síntese dos enunciados
EXERCÍCIO 01
Construção de Superfícies complexas a partir da Morfogénese de Cefalópodes
Tendo em conta que a forma geométrica de cada uma destas conchas é definida por meio de duas diretrizes planas (espirais concêntricas) e por geratrizes definidas por círculos existentes em planos perpendiculares ao plano que contém as directrizes.
EX01.1 Morfogénese: Spirula
EX01.2 Morfogénese: Planorbis
EX01.3 Morfogénese: Nautilus



EX01.1 Morfogénese: Spirula
No caso da Spirula, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior e o ponto A ao seu quadrante direito;
- pelo ponto O, no centro da figura anterior, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a espiral exterior tem centro no ponto O e raio maior no ponto A (15 unidades);
- a espiral interior tem centro também em O e o raio maior é igual a 10 unidades (o seu extremo é o ponto B);
- o número de voltas de ambas as espirais é igual a 2 e ambas se desenvolvem no sentido horário (do centro para o exterior);
- a geratriz é definida por uma circunferência vertical, cujo diâmetro passa pelos pontos A e B.


EX01.2 Morfogénese: Planorbis
No caso do Planorbis, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- para se construir a espiral que irá servir de base à morfogénese da concha é necessário fazer 4 construções auxiliares
- fase I
- desenhar quatro circunferências verticais cujos diâmetros são respectivamente 1, 2, 4 e 8 unidades;
- estes círculos são desenhados, partindo do ponto O até terminar no ponto A e os seus quadrantes são coincidentes entre si;
- estas circunferências fazem parte das geratrizes que definem a forma final;
- fase ii
- desenhar mais três circunferências verticaiscujos diâmetros são respectivamente 1,5 ; 3,0; e 6,0 unidades;
- estes círculos são desenhados, partindo do ponto O para o ponto H e os seus quadrantes também são coincidentes entre si;
- estas circunferências fazem parte das geratrizes que definem a forma final;
- fase III
- defina o pontos B como o quadrante do lado esquerdo do círculo de 6 unidades de diâmetro;
- defina os pontos D, F para os quadrantes que se intersectam na fase II;
- defina os pontos G, E, C para os quadrantes que se intersectam na fase I;
- desenhe vários círculos planos segundo pontos do seu diâmetro (AB, BC, CD, DE, EF, FG e GO);
- fase IV
- desenhe uma linha de H a A
- corte os círculos definidos na fase III pela linha da fase IV, eliminando a parte do quadrante inferior dos círculos AB, CD, EF e GO, e a parte do quadrante superior dos círculos BC, DE e FG.
- os segmentos resultantes dos cortes definidos anteriormente são as directrizes para o planorbis.
EX01.3 Morfogénese: Nautilus
No caso da Nautilus, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a espiral directriz é igual ao do exercício 1.2
- as geratrizes são círculos verticais definidos segundo dois pontos que contêm o respectivo diâmetro
- serão utilizadas 4 geratrizes, que têm em comum o ponto O e cujo diâmetro é respetivamente de 1, 3, 7 e 15 unidades;
- a segunda espiral directriz é definida através dos pontos do quadrante superior das 4 geratrizes e pelo ponto O.

EXERCÍCIO 02
Construção de Superfícies complexas a partir da Morfogénese de Gastrópodes
Tendo em conta que a forma geométrica de cada uma destas conchas é definida por meio de duas diretrizes (uma espiral plana e uma espiral torta assente sobre uma superfície de revolução ou por um eixo vertical) e por geratrizes definidas por círculos existentes em planos perpendiculares ao plano horizontal
EX02.1 Morfogénese: Caracol
EX02.2 Morfogénese: Caramujo
EX02.3 Morfogénese: Búzio



EX02.1 Morfogénese: Caracol
No caso do Caracol, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior e o ponto A ao seu quadrante direito;
- pelo ponto O, no centro da figura anterior, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a geometria desta concha é definida por 4 círculos verticais;
- o maior dos círculos têm um diâmetro de 15 unidades e passa pelo ponto O e A
- o ponto B é definido pelo quadrante superior do circulo OA anterior
- o ponto V, é definido pela lina horizontal perpendicular ao eixo OP que passa pelo ponto B
- as demais geratrizes têm diâmetros, respectivamente, de 1, 3 e 7 unidades e são tangentes ao eixo vertical OP e à linha VB
- a primeira directriz é a gerada por uma espiral plana análoga, mas não igual em dimensão, àquela defenida no exercício 1.3, que é projetada sobre uma superfície de revolução auxiliar;
- a superfície de revolução auxiliar é definida pelo eivo vertical OP e pela geratriz AV;
- a segunda directriz é o segmento vertical definido entre os pontos OV.


EX02.2 Morfogénese: Caramujo
No caso do Caramujo, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 35 unidades, cujo topo é o ponto P;
- uma das geratrizes é um circulo vertical definido pelo seu diâmetro, através dos pontos OA
- as demais geratrizes têm raios iguais a 3,5; 1,5 e 0,5 unidades e são sempre tangentes ao eixo vertical OP e à secção anterior
EX02.3 Morfogénese: Búzio
No caso da Nautilus, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a espiral directriz é igual ao do exercício 1.2
- as geratrizes são definidas por um quadrado de 15 x 15 unidades, o qual se encontra dividido por dois quadrados, respectivamente no canto superior esquerdo e no canto inferior direito
- o quadrado do canto superior esquerdo tem 3 x3 unidades e contem um quarto de circulo cujo centro é o canto inferior direito
- o quadrado do canto inferior direito tem 12 x 12 unidades e contei um quarto de circulo cujo centro é o seu canto superior esquerdo
- no canto superior direito existe um rectângulo de 12 x 3 unidades, o qual contem um arco de clips, com centro no sei canto inferior esquerdo e raios iguais aos lados
- ao prolongar-se o lado esquerdo do quadrado de 15 x 15 unidades, este vai ser tangente a um circulo de raio igual a 15 unidades , o qual também é tangente ao arco existente no quadrado de 12 x 12 unidades
- as geometrias existentes no quadrado de 3 x 3 e no rectângulo de 12 x 3 devem ser unidas, correspondendo o lado esquerdo ao ponto O e o lado direito ao ponto A
- as geometria resultantes do prolongamento do lado esquerdo do quadrado de 15 x 15, do circulo de r= 15 e do quadrado de 12 x 12 devem ser unidas numa única curva, sendo o seu extremo inferior esquerdo o ponto P e o seu extremo direito o ponto A
- estas duas últimas figuras geométricas devem se rodadas 90 segundo a charneira definida pelos pontos OA
- a superfície de revolução auxiliar é um arco de elipse (1/4) vertical com centro no ponto O, semi-eixo horizontal em A e semi-eixo vertical com 5 unidades.

EXERCÍCIO 03
Construção de Superfícies complexas a partir da Morfogénese de Bivalves
Tendo em conta que a forma geométrica de cada uma destes bivalves é definida por meio de duas diretrizes (uma semicircunferência vertical e uma curva cónica) e por geratrizes definidas no plano horizontal
EX03.1 Morfogénese: Mexilhão
EX03.2 Morfogénese: Vieira
EX03.3 Morfogénese: Ostra



EX03.1 Morfogénese: Mexilhão
No caso do Mexilhão, sabe-se que:
- o rectângulo que contêm a forma em planta tem 8 x 20 unidades
- dentro desse rectângulo existem mais 4 sub-rectângulos localizados nos extremos
- o sub-rectângulo do canto inferior esquerdo é um quadrado com 3x3 unidades
- o sub-rectângulo do canto inferior direito é um quadrado com 5x5 unidades
- o sub-rectângulo do canto superior esquerdo tem 3 x 17 unidaes
- o sub-rectângulo do canto superior direito tem 5 x 15 unidades
- nas figuras que são quadrados gere um arco de circunferência
- nas figuras que são rectângulos, gere elipse
- por fim una os quatro segmentos numa única curva


EX03.2 Morfogénese: Vieira
No caso do Vieira (nervuras), sabe-se que:
- em planta a vieira é definida por um rectângulo de 10 x 9 unidades
- o rectângulo anterior é subdividido em 4 rectângulos mais pequenos, localizados em cada um dos extremos
- nos extremos inferiores os sub-rectângulos são quadrados de 5 x 5 unidades
- nos extremos superiores os sub-rectângulos têm 4 x 5 unidades
- existe ainda um quinto sub-rectângulo de 4 x 2 unidades em que o centro coincide com o ponto médio do segmento superior do rectângulo envolvente
- nos sub-rectângulos são quadrados de 5 x 5 unidades gere dois arcos de circunferência
- nos sub-rectângulos têm 4 x 5 unidades gere dois arcos de elipse
- uma a quinta sub-rectângulo às elipses
- uma as dois arcos de circunferência por forma a gerar um semicirculo
- subdivida-o em 25 partes e faça passar por cada dois pontos um circulo
- corte os últimos círculos segundo o semicírculo anterior
- junte todas as semicircunferências com as elipses
EX03.3 Morfogénese: Ostra
No caso da Ostra, sabe-se que:
- o rectângulo que contem forma em planta tem 20 unidades (em X) por 9 unidades (em Y)
- subdivida o rectângulo anterior em 6 subrectângulos
- gere um rectângulo de 5 x 10 unidades por forma a coincidir com os cantos inferiores esquerdo e direito;
- em cada um destes dois rectângulos gere um arco e elipse
- a parte superior é definida por 4 rectângulos, todos com 4 x 5 unidades
- nos rectângulos dos extremos superiores gere arcos de elipse
- e nos rectângulos centrais dos segmentos de recta, coincidentes com a parte superior desses mesmo retângulos
- uma os dois segmentos de elipse existentes no lado esquerdo e repita o processo para o lado direito
- faça passar pós cada uma das anteriores curvas unidas uma espiral segundo uma curva, definindo que o raio inicial (no ponto médio inferior) tem um raio de 1 unidade e que no outro extremo um raio com 0 unidades

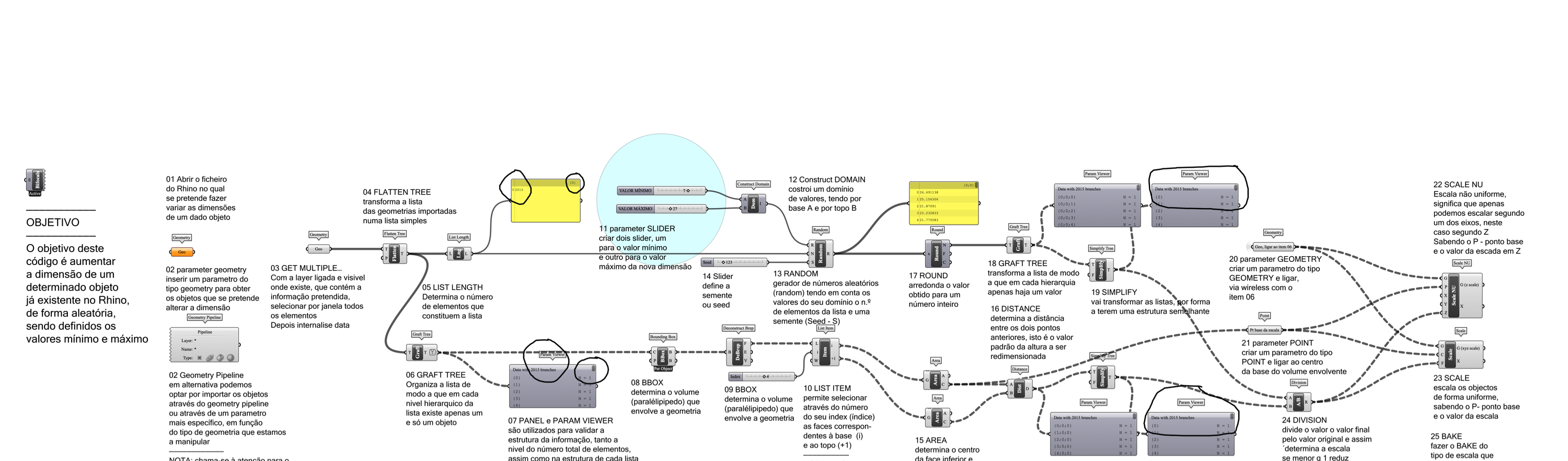
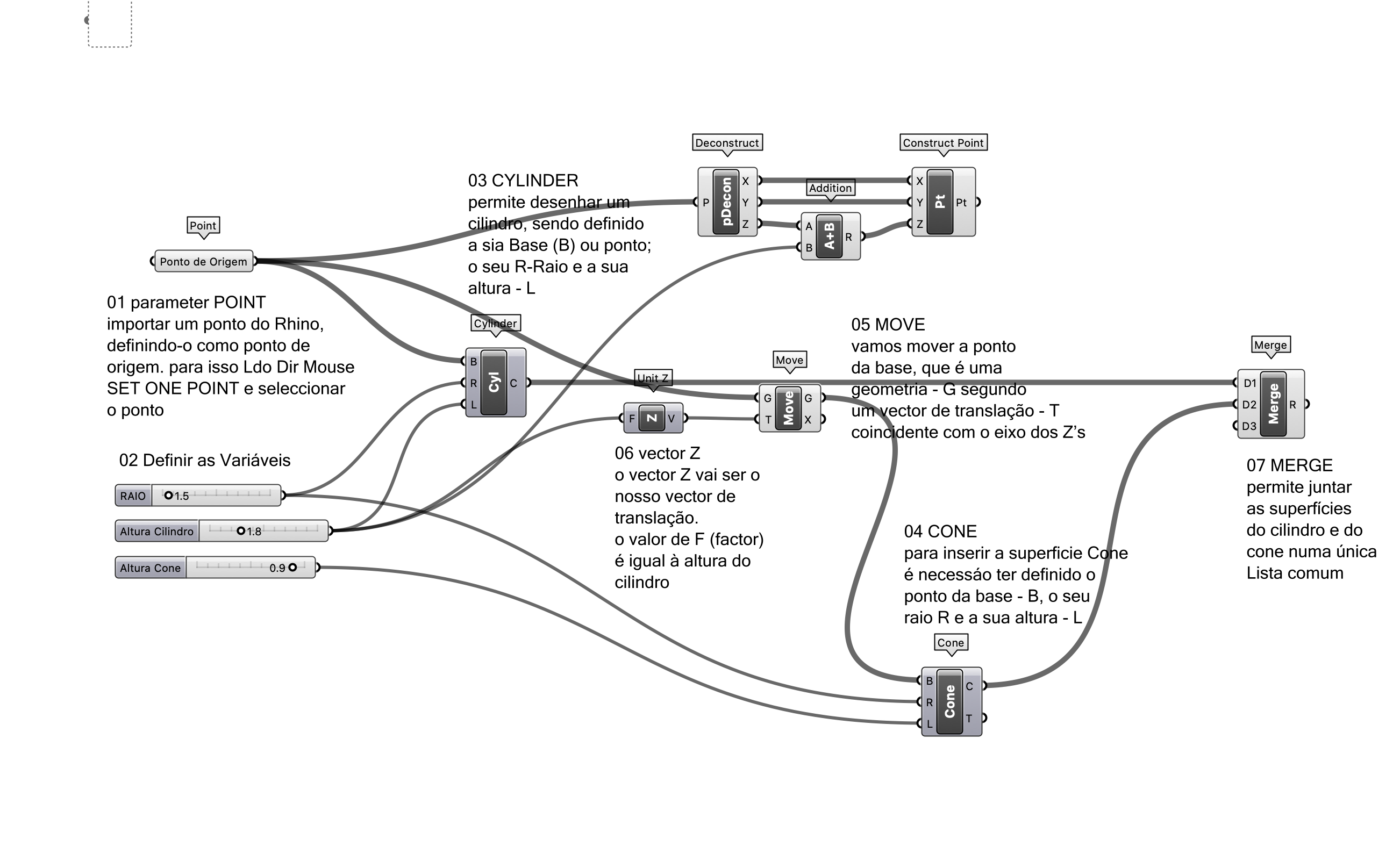
EXERCÍCIO 04
EX04 Bungalow paramétrico
Construção paramétrica de um "Bungalow"
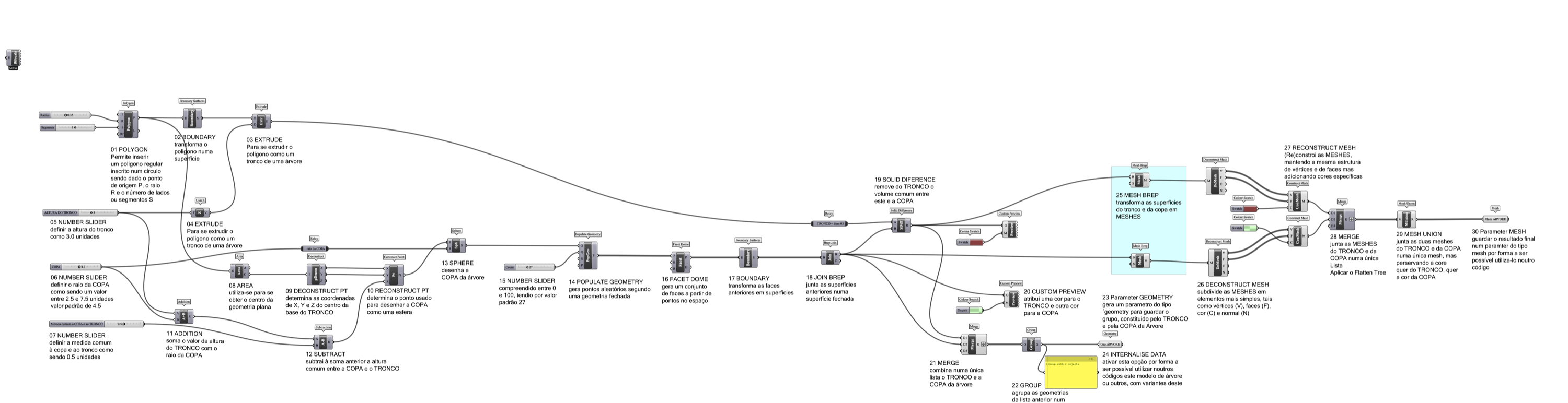
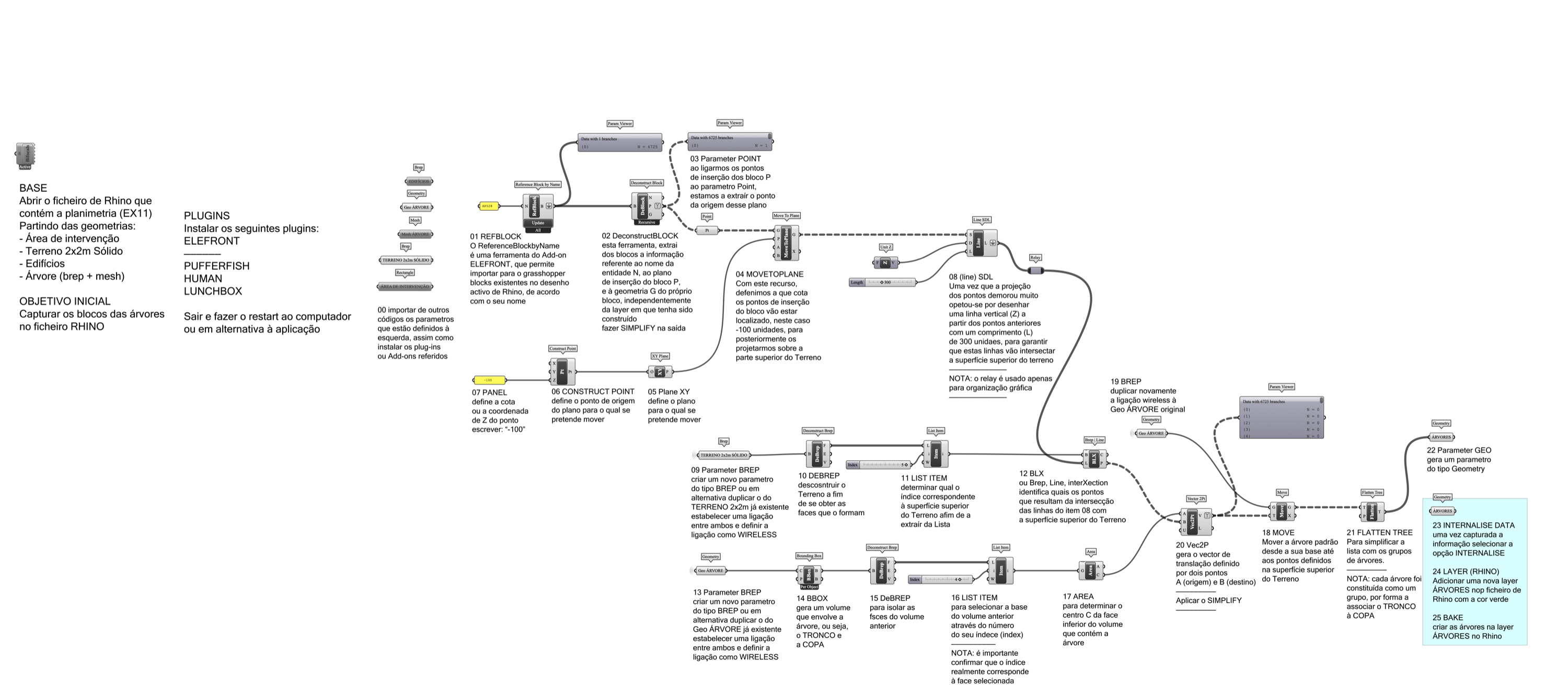
Tendo em conta que um bangalô pode ser o resultado da adição de um cilindro com um cone, construa o código paramétrico em Grasshopper sabendo que:
- o valor do raio pode varias entre 1 e 10,0 unidades
- o valor da altura do cilindro pode variar entre 0,5 e 5 unidades
- o valor da altura do cone pode variar entre 0,1 e 1 unidade
- o ponto ou pontos da base do cilindro são definidos directamente no treino, de forma aleatória, quer na sua localização, quer no seu número

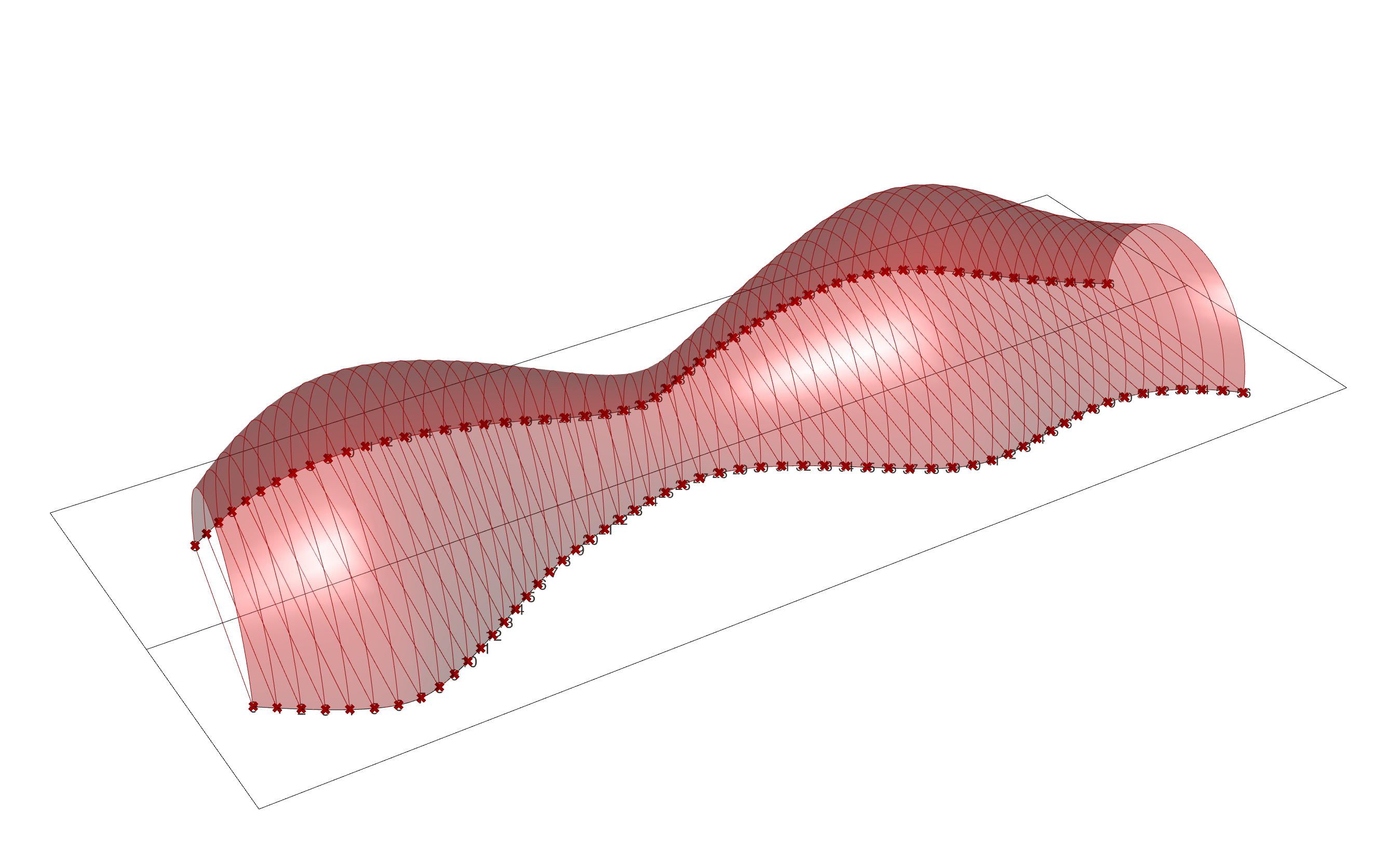
EXERCÍCIO 05
EX05 Abrigo paramétrico
Construção de um abrigo paramétrico
Construa um abrigo paramétrico, sabendo que:
- o abrigo é definido por duas curvas planas inseridas em dois rectângulos de 10 x 50 unidades que partilham uma aresta de 50 unidades
- a superfície é definida pelos arcos de circunferência verticais gerados a partir da subdivisão das curvas plandas
- a divisão das curvas varia entre 1 e 100 unidades
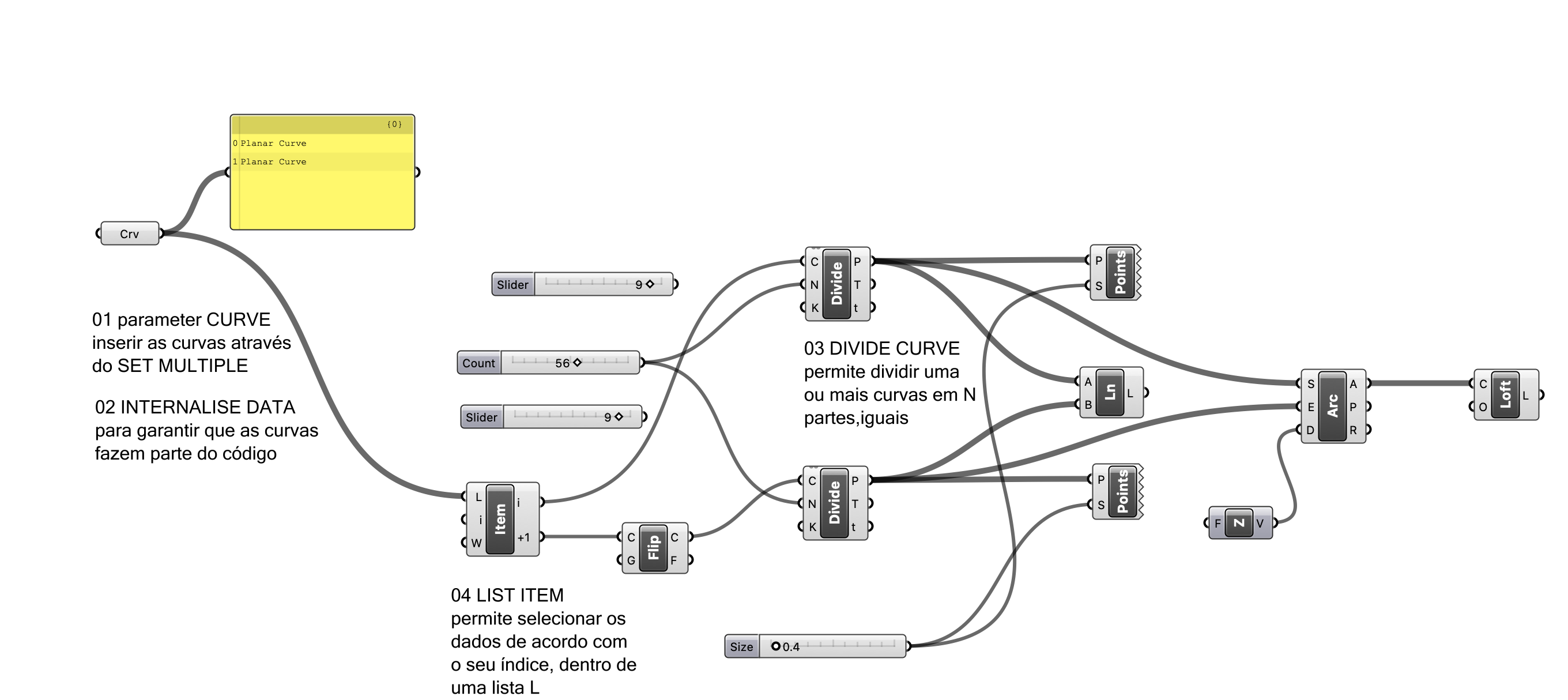
EXERCÍCIO 06
EX06 Casa paramétrica
Construção de uma casa paramétrica inserindo os elementos: porta, janela e chaminé
Construa uma casa paramétrico, sabendo que esta está dividida em 4 fases (I, II, III, e IV):
FASE I - casa
- a casa é definida por 5 pontos (A, B, C, D e E)
- o ponto A corresponde à origem do desenho (0,0,0) e está localizada no canto inferior esquerdo
- o ponto B corresponde ao canto superior esquerdo, ou seja à parte superior do cunhal esquerdo da casa
- o ponto C corresponde à cimeeira do telhado, isto é ao ponto de maior cota
- o ponto D corresponde ao canto direito (ao longo do eixo dos X), ou seja à parte superior do cunhal direito da casa
- o ponto E corresponde ao canto inferior direito (segundo o eixo dos X) da casa
- as dimensões da casa são definidas pelas variáveis WW, WH, WD, RH e RP
- a variável WW - wallwidth, corresponde à largura, segundo o eixo dos X, da casa e tem uma amplitude de [1<15.0]
- a variável WH - wallheight, corresponde à altura (do cunhal) da casa e tem uma amplitude de [0<12.0]
- a variável WD - walldepth, corresponde à profundidade da casa e tem uma amplitude de [2<20.0]
- a variável RH - roofheight, corresponde à altura do telhado (medido na vertical do cunhal à comeria) da casa e tem uma amplitude de [0<18.0]
- a variável RP - roofposition, corresponde à posição relativa da cumeeira do telhado (ponto C) da casa e tem uma amplitude de [0<1.000]. Pelo que pode oscilar desde o alinhamento vertical do ponto B ao pondo D


FASE II - porta
- a porta deverá ser inserida na fachada que contem o plano XY
- a porta é definida pelas variáveis DP, DW, DH, DTH
- a variável DP - doorposition, corresponde à posição relativa da porta na fachada definida pelo plano XY da casa e tem uma amplitude de [0<1.000]. Pelo que pode oscilar desde o ponto A ao ponto E
- a variável DW - doorwidth, corresponde à largura da porta da casa e tem uma amplitude de [0.2<15]
- a variável DH - doorwidth, corresponde à largura da porta da casa e tem uma amplitude de [1<18.0]
- a variável DTH- doorthickness, corresponde à espessura da porta da casa e tem uma amplitude de [0.4<1]
- a porta deve ser desenhada utilizando o componente boxrectangle
FASE III - janela
- ◆ a janela deverá ser inserida na fachada que contem o plano YZ, definido pelo ponto de origem em E
- a janela é definida pelas variáveis JP, JE, JW, JH, JTH
- a variável JP - janelaposition, corresponde à posição relativa da janela na fachada definida pelo plano YZ que passa pelo ponto E da casa e tem uma amplitude de [0<1.000]. Pelo que pode oscilar ao longo de toda a profundidade da casa (WD)
- a variável JE - janelaelevation, corresponde à elevação (altura) ao solo da janela da casa e tem uma amplitude de [0<18.0]
- a variável JW - janelawidth, corresponde à largura da janela da casa e tem uma amplitude de [0.2<20]
- a variável JH - janelawidth, corresponde à altura da janela da casa (propriamente dita) e tem uma amplitude de [0<18.0]
- a variável JTH- janelathickness, corresponde à espessura da janela da casa e tem uma amplitude de [0.4<1]
- a janela deve ser desenhada utilizando o componente boxrectangle


FASE IV - chaminé
- a chaminé deverá ser inserida implantação da casa (plano XY)
- a chaminé é definida pelas variáveis PX, PY, XW, XH, XTH
- a variável PX - positionX, corresponde à posição relativa da chaminé ao longo do eixo dos X, que vai do ponto A ao ponto E da casa e tem uma amplitude de [0<1.000]
- a variável PY - positionY, corresponde à posição relativa da chaminé ao longo do eixo dos Y, que vai do ponto B até ao limite da sua profundidade da casa e tem uma amplitude de [0<1.000]
- a variável XH - chaminéheight, corresponde à altura da chaminé da casa medida a partir do plano XY com origem ca comeria (ponto C) e tem uma amplitude de [0.5<5]
- a variável XW - chaminéwidth, corresponde à largura da chaminé (segundo o eixo dos X) da casa e tem uma amplitude de [0.5<5]
- a variável XTH- chaminéthickness, corresponde à profundidade da chaminé (segundo o eixo dos Y) da casa e tem uma amplitude de [0.5<5]
- a chaminé deve ser desenhada utilizando o componente boxrectangle
- o volume correspondente à chaminé deverá ser desenhado a partir do plano XY que passa pelo ponto A ou pelo ponto B
EXERCÍCIO 07
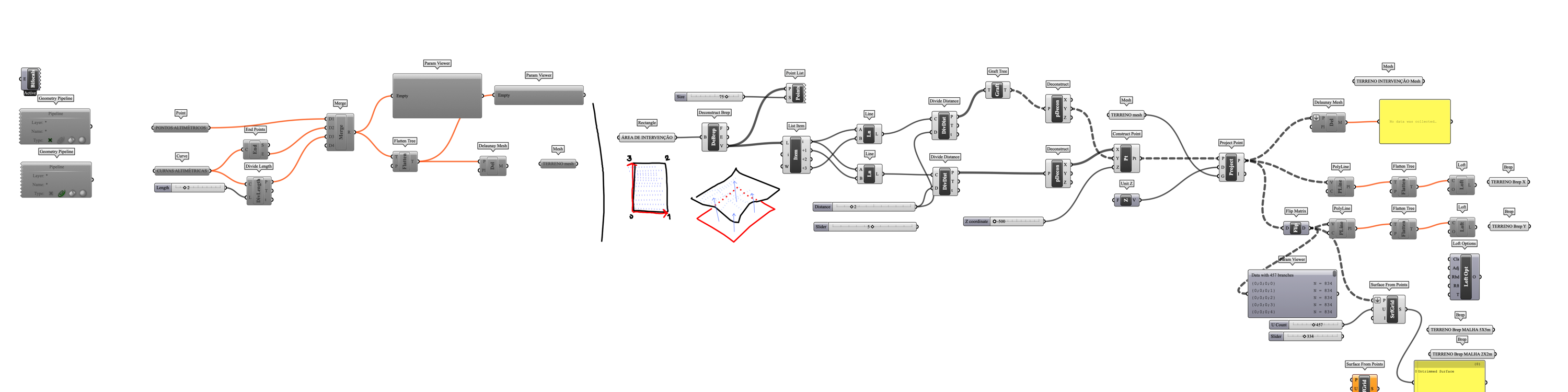
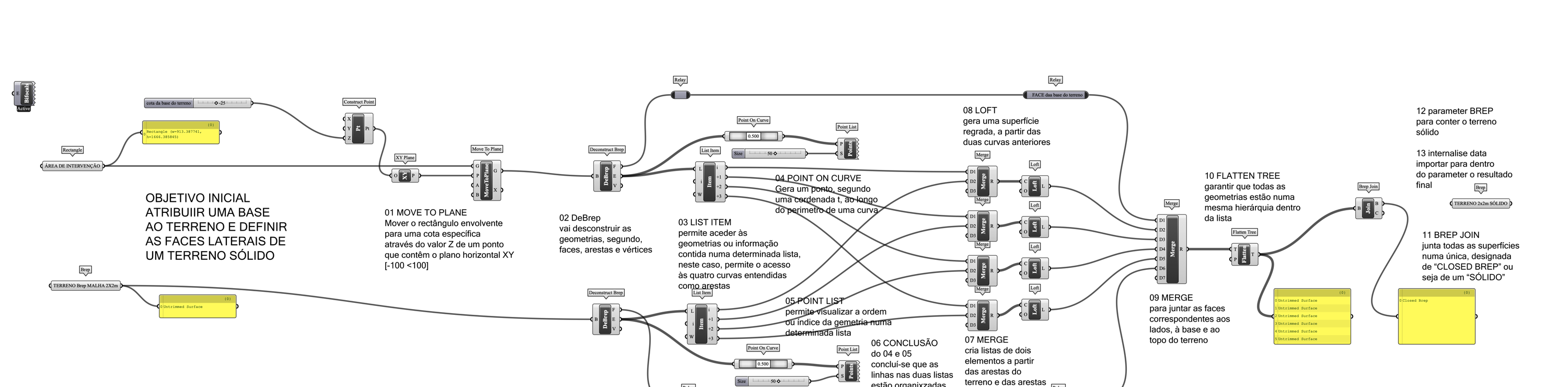
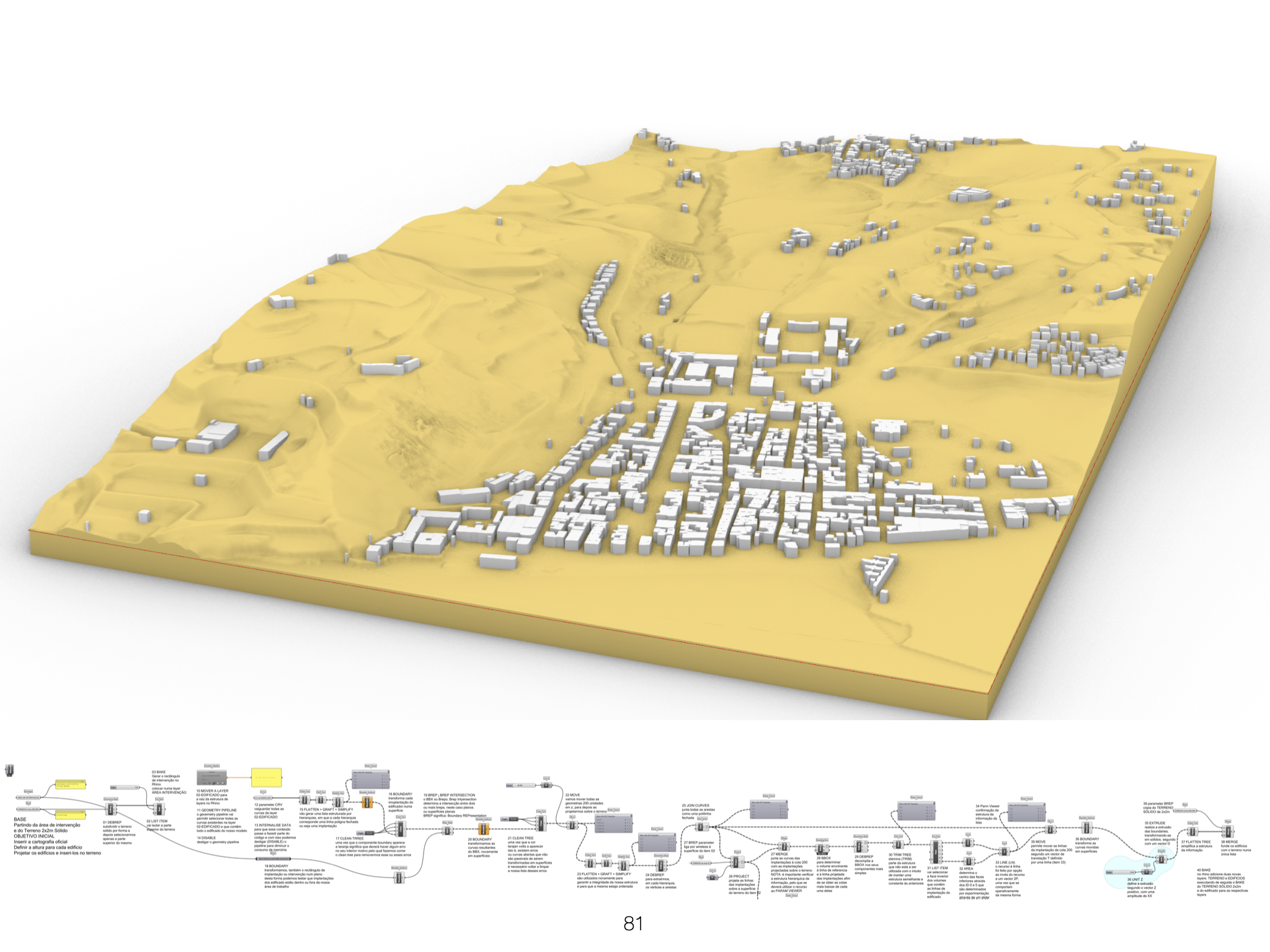
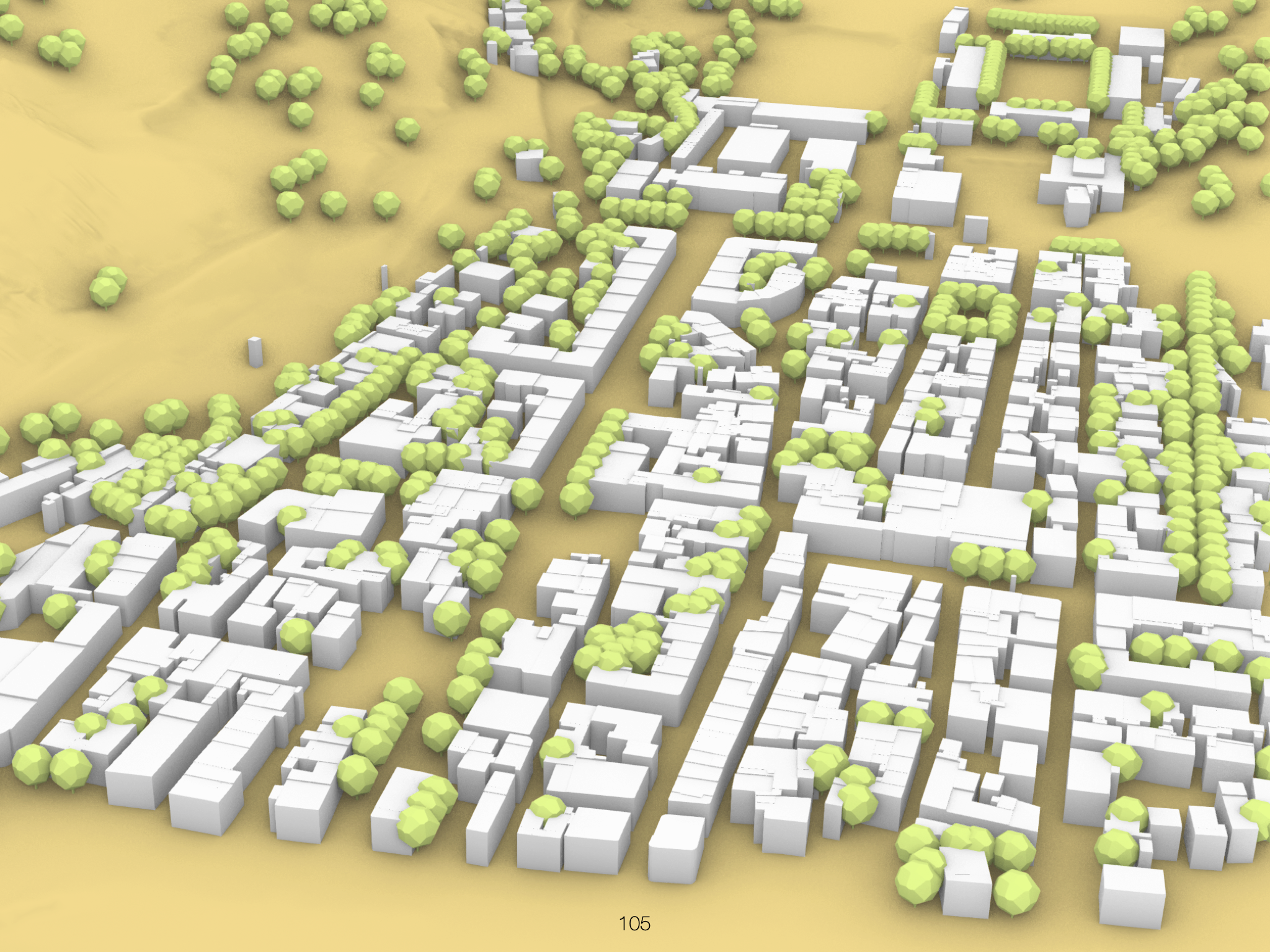
EX07 Terreno paramétrico
Construção de um terreno paramétrico a partir de desenhos altimétricos em formato DWG
Construa um terreno paramétrico, sabendo que:
- o terreno é definido por uma nuvem de pontos
- a nuvem de pontos é obtida a partir de pontos altimétricos, curvas de nível e linhas de talude
- os pontos altimétricos, curvas de nível e linhas de talude estão definidos em desenhos DWG
- Os desenhos a utilizar são os seguintes:
- Carta 04C - Alt.dwg
- Carta 04D - Alt.dwg
- Carta 04E - Alt.dwg
- Carta 05C - Alt.dwg
- Carta 05D - Alt.dwg
- Carta 05E - Alt.dwg
- Carta 06C - Alt.dwg
- Carta 06D - Alt.dwg
- Carta 06E - Alt.dwg
- Carta 07C - Alt.dwg
- Carta 07D - Alt.dwg
- Carta 07E - Alt.dwg


EXERCÍCIO 08
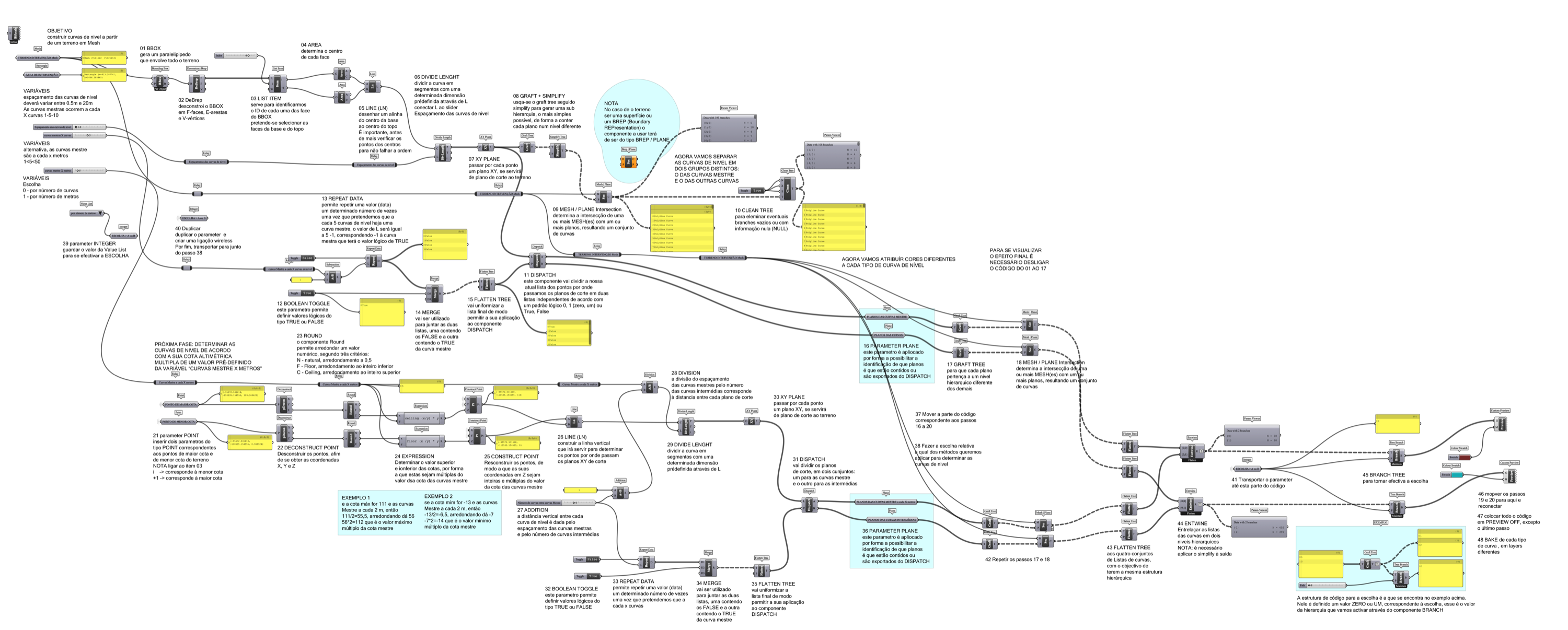
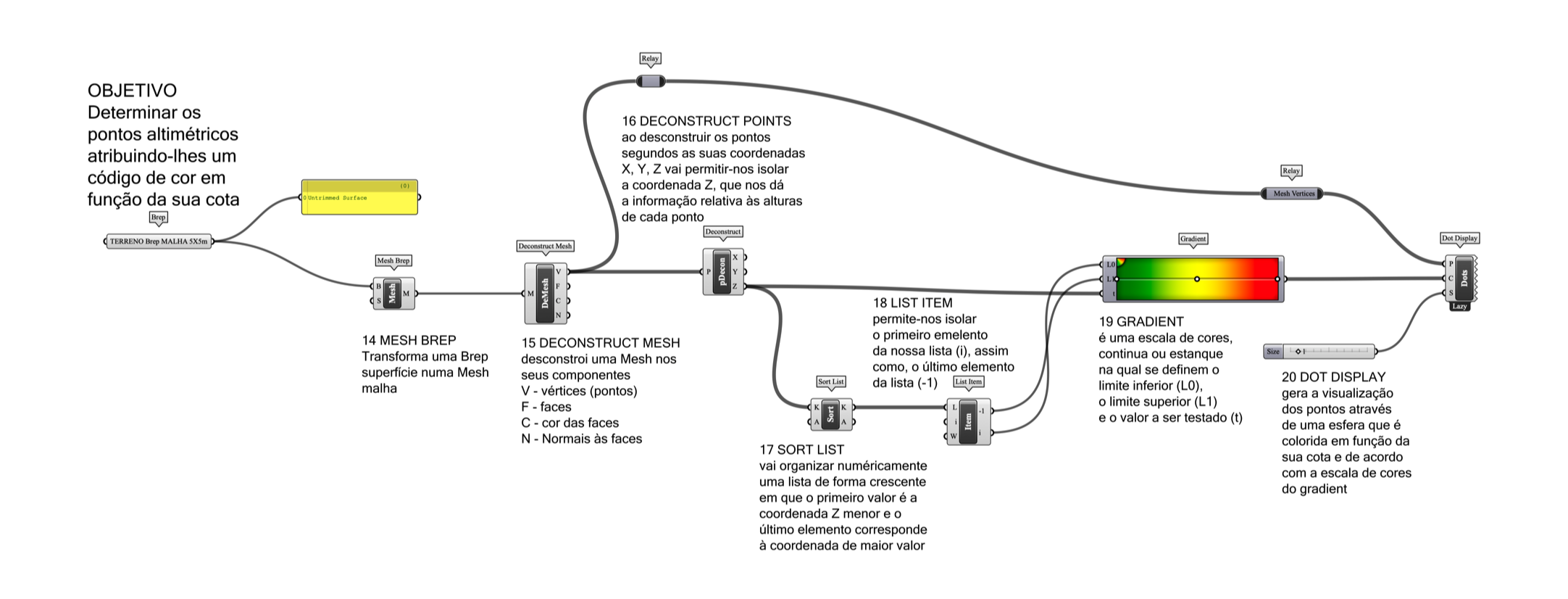
EX08 MESH to CONTOUR
Construção de curvas de nivel a partir de um terreno em Mesh
Construa um algoritmo paramétrico, a partir de um ficheiro de um terreno dado, em MESH
link para o ficheiro do terreno…