Tendo em conta que a forma geométrica de cada uma destas conchas é definida por meio de duas diretrizes planas (espirais concêntricas) e por geratrizes definidas por círculos existentes em planos perpendiculares ao plano que contém as directrizes.

No caso da Spirula, sabe-se que:

• a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
• o ponto O corresponde ao centro da figura anterior e o ponto A ao seu quadrante direito;
• pelo ponto O, no centro da figura anterior, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
• a espiral exterior tem centro no ponto O e raio maior no ponto A (15 unidades);
• a espiral interior tem centro também em O e o raio maior é igual a 11 unidades (o seu extremo é o ponto B);
• o número de voltas de ambas as espirais é igual a 3 e ambas se desenvolvem no sentido horário (do centro para o exterior);
• a geratriz é definida por uma circunferência vertical, cujo diâmetro passa pelos pontos A e B.

No caso do Planorbis, sabe-se que:

• a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
• o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
• pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
• para se construir a espiral que irá servir de base à morfogénese da concha é necessário fazer 4 construções auxiliares
• fase I
• desenhar quatro circunferências verticais cujos diâmetros são respectivamente 1, 2, 4 e 8 unidades;
• estes círculos são desenhados, partindo do ponto O até terminar no ponto A e os seus quadrantes são coincidentes entre si;
• estas circunferências fazem parte das geratrizes que definem a forma final;
• fase ii
• desenhar mais três circunferências verticaiscujos diâmetros são respectivamente 1,5 ; 3,0; e 6,0 unidades;
• estes círculos são desenhados, partindo do ponto O para o ponto H e os seus quadrantes também são coincidentes entre si;
• estas circunferências fazem parte das geratrizes que definem a forma final;
• fase III
• defina o pontos B como o quadrante do lado esquerdo do círculo de 6 unidades de diâmetro;
• defina os pontos D, F para os quadrantes que se intersectam na fase II;
• defina os pontos G, E, C para os quadrantes que se intersectam na fase I;
• desenhe vários círculos planos segundo pontos do seu diâmetro (AB, BC, CD, DE, EF, FG e GO);
• fase IV
• desenhe uma linha de H a A
• corte os círculos definidos na fase III pela linha da fase IV, eliminando a parte do quadrante inferior dos círculos AB, CD, EF e GO, e a parte do quadrante superior dos círculos BC, DE e FG.
• os segmentos resultantes dos cortes definidos anteriormente são as directrizes para o planorbis.

No caso da Nautilus, sabe-se que:

• a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
• o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
• pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
• a espiral directriz é igual ao do exercício 1.2
• as geratrizes são círculos verticais definidos segundo dois pontos que contêm o respectivo diâmetro
• serão utilizadas 4 geratrizes, que têm em comum o ponto O e cujo diâmetro é respetivamente de 1, 3, 7 e 15 unidades;
• a segunda espiral directriz é definida através dos pontos do quadrante superior das 4 geratrizes e pelo ponto O.

Tendo em conta que a forma geométrica de cada uma destas conchas é definida por meio de duas diretrizes (uma espiral plana e uma espiral torta assente sobre uma superfície de revolução ou por um eixo vertical) e por geratrizes definidas por círculos existentes em planos perpendiculares ao plano horizontal

No caso do Caracol, sabe-se que:

• a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
• o ponto O corresponde ao centro da figura anterior e o ponto A ao seu quadrante direito;
• pelo ponto O, no centro da figura anterior, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
• a geometria desta concha é definida por 4 círculos verticais;
• o maior dos círculos têm um diâmetro de 15 unidades e passa pelo ponto O e A
• o ponto B é definido pelo quadrante superior do circulo OA anterior
• o ponto V, é definido pela lina horizontal perpendicular ao eixo OP que passa pelo ponto B
• as demais geratrizes têm diâmetros, respectivamente, de 1, 3 e 7 unidades e são tangentes ao eixo vertical OP e à linha VB
• a primeira directriz é a gerada por uma espiral plana análoga, mas não igual em dimensão, àquela defenida no exercício 1.3, que é projetada sobre uma superfície de revolução auxiliar;
• a superfície de revolução auxiliar é definida pelo eivo vertical OP e pela geratriz AV;
• a segunda directriz é o segmento vertical definido entre os pontos OV.

No caso do Caramujo, sabe-se que:

• a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
• o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
• pelo ponto O, passa um eixo vertical com 35 unidades, cujo topo é o ponto P;
• uma das geratrizes é um circulo vertical definido pelo seu diâmetro, através dos pontos OA
• as demais geratrizes têm raios iguais a 3,5; 1,5 e 0,5 unidades e são sempre tangentes ao eixo vertical OP e à secção anterior

No caso da Nautilus, sabe-se que:

• a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
• o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
• pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
• a espiral directriz é igual ao do exercício 1.2
• as geratrizes são definidas por um quadrado de 15 x 15 unidades, o qual se encontra dividido por dois quadrados, respectivamente no canto superior esquerdo e no canto inferior direito
• o quadrado do canto superior esquerdo tem 3 x3 unidades e contem um quarto de circulo cujo centro é o canto inferior direito
• o quadrado do canto inferior direito tem 12 x 12 unidades e contei um quarto de circulo cujo centro é o seu canto superior esquerdo
• no canto superior direito existe um rectângulo de 12 x 3 unidades, o qual contem um arco de clips, com centro no sei canto inferior esquerdo e raios iguais aos lados
• ao prolongar-se o lado esquerdo do quadrado de 15 x 15 unidades, este vai ser tangente a um circulo de raio igual a 15 unidades , o qual também é tangente ao arco existente no quadrado de 12 x 12 unidades
• as geometrias existentes no quadrado de 3 x 3 e no rectângulo de 12 x 3 devem ser unidas, correspondendo o lado esquerdo ao ponto O e o lado direito ao ponto A
• as geometria resultantes do prolongamento do lado esquerdo do quadrado de 15 x 15, do circulo de r= 15 e do quadrado de 12 x 12 devem ser unidas numa única curva, sendo o seu extremo inferior esquerdo o ponto P e o seu extremo direito o ponto A
• estas duas últimas figuras geométricas devem se rodadas 90 segundo a charneira definida pelos pontos OA
• a superfície de revolução auxiliar é um arco de elipse (1/4) vertical com centro no ponto O, semi-eixo horizontal em A e semi-eixo vertical com 5 unidades.

Tendo em conta que a forma geométrica de cada uma destes bivalves é definida por meio de duas diretrizes (uma semicircunferência vertical e uma curva cónica) e por geratrizes definidas no plano horizontal

No caso do Mexilhão, sabe-se que:

• o rectângulo que contêm a forma em planta tem 8 x 20 unidades
• dentro desse rectângulo existem mais 4 sub-rectângulos localizados nos extremos
• o sub-rectângulo do canto inferior esquerdo é um quadrado com 3x3 unidades
• o sub-rectângulo do canto inferior direito é um quadrado com 5x5 unidades
• o sub-rectângulo do canto superior esquerdo tem 3 x 17 unidaes
• o sub-rectângulo do canto superior direito tem 5 x 15 unidades
• nas figuras que são quadrados gere um arco de circunferência
• nas figuras que são rectângulos, gere elipse
• por fim una os quatro segmentos numa única curva

No caso do Vieira (nervuras), sabe-se que:

• em planta a vieira é definida por um rectângulo de 10 x 9 unidades
• o rectângulo anterior é subdividido em 4 rectângulos mais pequenos, localizados em cada um dos extremos
• nos extremos inferiores os sub-rectângulos são quadrados de 5 x 5 unidades
• nos extremos superiores os sub-rectângulos têm 4 x 5 unidades
• existe ainda um quinto sub-rectângulo de 4 x 2 unidades em que o centro coincide com o ponto médio do segmento superior do rectângulo envolvente
• nos sub-rectângulos são quadrados de 5 x 5 unidades gere dois arcos de circunferência
• nos sub-rectângulos têm 4 x 5 unidades gere dois arcos de elipse
• uma a quinta sub-rectângulo às elipses
• uma as dois arcos de circunferência por forma a gerar um semicirculo
• subdivida-o em 25 partes e faça passar por cada dois pontos um circulo
• corte os últimos círculos segundo o semicírculo anterior
• junte todas as semicircunferências com as elipses

No caso da Ostra, sabe-se que:

• o rectângulo que contem forma em planta tem 20 unidades (em X) por 9 unidades (em Y)
• subdivida o rectângulo anterior em 6 subrectângulos
• gere um rectângulo de 5 x 10 unidades por forma a coincidir com os cantos inferiores esquerdo e direito;
• em cada um destes dois rectângulos gere um arco e elipse
• a parte superior é definida por 4 rectângulos, todos com 4 x 5 unidades
• nos rectângulos dos extremos superiores gere arcos de elipse
• e nos rectângulos centrais dos segmentos de recta, coincidentes com a parte superior desses mesmo retângulos
• uma os dois segmentos de elipse existentes no lado esquerdo e repita o processo para o lado direito
• faça passar pós cada uma das anteriores curvas unidas uma espiral segundo uma curva, definindo que o raio inicial (no ponto médio inferior) tem um raio de 1 unidade e que no outro extremo um raio com 0 unidades

Tendo em conta que a forma geométrica definida por um Kinguio / Oranda por meio de duas diretrizes (correspondentes à linha dorsal e ventral definidas num plano de Frente) e por geratrizes definidas de acordo com três possíveis secções transversais existentes em planos de topo

use a loupe, movendo o mouse para ver em detalhe, ou em alternativa clique sobre a imagem para ter acesso à imagem em fundo branco, em formato PNG

No caso das secções longitudinais, correspondentes às linhas dorsal e ventral, sabe-se que:

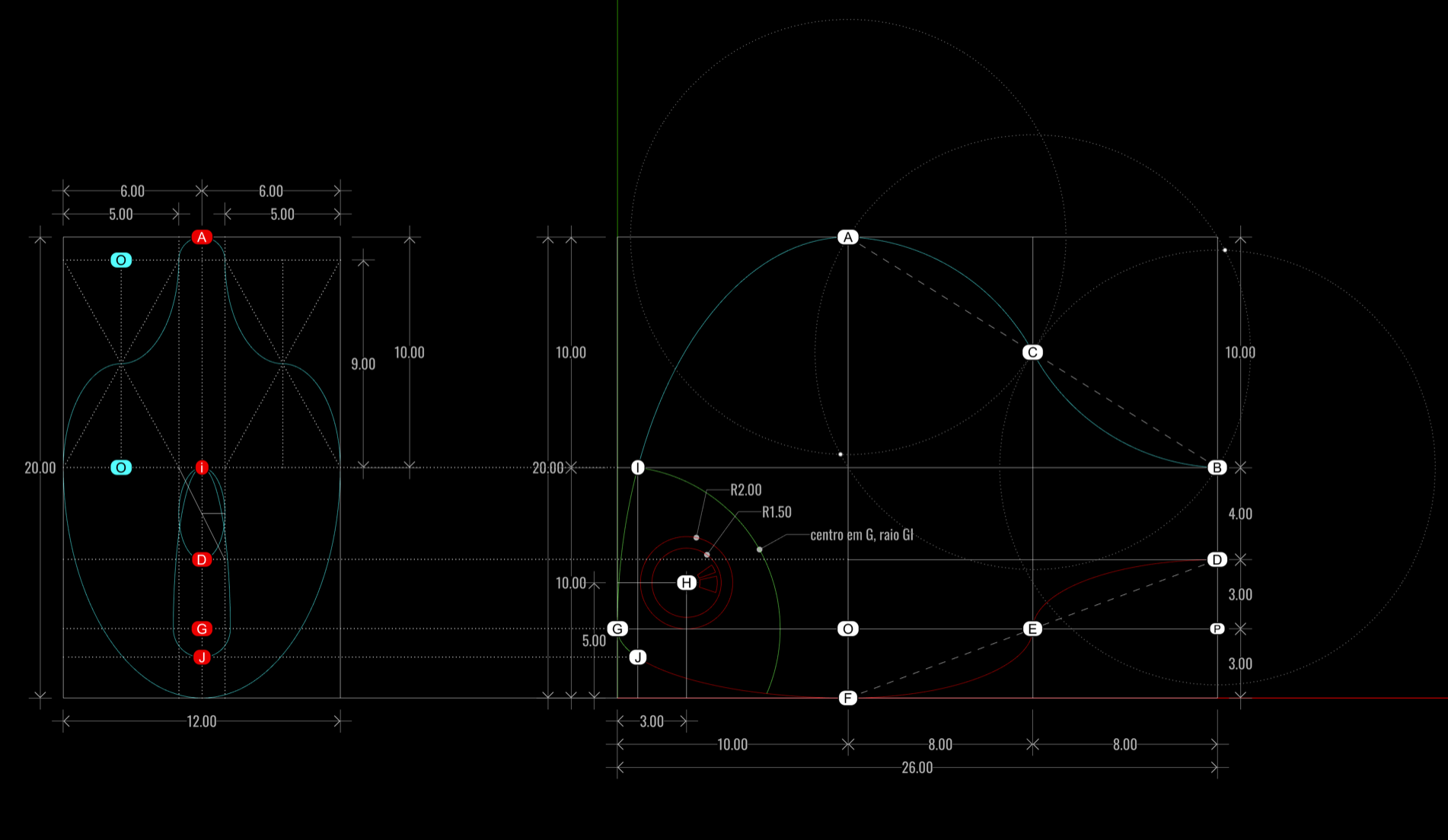
• o perfil longitudinal, definido na figura abaixo está inscrito num rectângulo de 26 x 20 unidades
• no seu interior existem mais 11 rectângulos, seis dos quais com 8x3 unidades, dois com 8x4 unidades e 8x10 unidades e um rectângulo com 10x3 e 10x17, conforme figura abaixo
• nesta estrutura são identificados os pontos A, B, C, D, E, Fe G
• os pontos O e P correspondem a centros de elipses auxiliares
• o ponto H corresponde ao centro dos círculos que define o globo ocular
• o ponto I corresponde à intersecção entre a linha horizontal que passa pelo ponto B e o arco de elipse definida pelos pontos OGA
• o ponto J é o resultado da intersecção entre a linha vertical que passa pelo ponto I e o arco de elipse definido pelos pontos OGF

No caso das secções transversais, correspondentes às secções, sabe-se que:

• existem três secções, definidas pelos planos transversais que contêm os pontos IJ, AF e BD
• a secção IJ é definida na parte inferior pela sem,i-circunferencia com dento em G e raio em J (vermelhos)
• a secção IJ é definida na parte superior pelo arco de elipse com centro em G (vermelho, um dos extremos da semicircunferência anterior e o ponto I (vermelho)
• a secção AF é definida por 6 partes
• a primeira parte (mais superior) é definida pelo semi-círculo com raio igual a 1 unidade cujo quadrante superior é o ponto A
• as 4 partes imediatamente abaixo são definidas por um arco e contra arco de elipse com centro nos pontos o (azuis)
• finalmente a parte inferior é uma semi-elipse com centro em I, raio maior igual a 10 e raio menor igual a 6 unidades
• a secção BD é definida pela Elipse cujo diâmetro passa pelos pontos I e D (vermelhos) e tem raio menor igual a 1 unidades

Com base no exercício anterior cada aluno deverá desenvolva um conjunto de 3 padrões bidimensionais, designados por A, B (B1 e B2) e C (C1 e C2)
Os padrões devem ser aplicados conforme indicado a seguir.

Com base no exercício anterior aplique o padrão A

Com base no exercício anterior aplique o padrão B1 e B2 de forma aleatória

Com base no exercício anterior aplique o padrão C1 e C2 de forma aleatória

Com base na estrutura do exercício 04 construir uma nova superfície a partir uma superfície plana e recorrendo apenas à manipulação de pontos através do duplo uso dos Control-point e do Rebuild

No caso da estruturas A, sabe-se que:

• Desenhe duas circunferências com o mesmo centro, em que uma das circunferências tem 2 unidades de raio e a outra 4 unidades
• copie as duas circunferências 12 unidades para o lado direito
• em cada um dos dois conjuntos de círculos desenhe uma linha vertical ao plano de trabalho com 6 unidades
• desenhe um arco de circunferência por forma a unir os extremos superiores das linhas verticais
• una os dois segmentos verticais ao arco de circunferência anterior
• desenhe quatro espirais à volta do eixo (figura anterior) partindo dos quadrantes esquerdo e direito de cada circulo, perfazendo uma volta
• gere duas superfícies, uma interior e outra exterior, com base nas directrizes definidas pelas espirais e pelas geratrizes definidas pelos círculos
• desenhe um padrão C e aplique-o à geometria

No caso da estruturas B, sabe-se que:

• parta da estrutura anterior (Exercício 07), definida pós duas superfícies geradas por quatro espirais e por quatro círculos
• desenhe o padrão B, definida na aula, e aplique-o à geometria

No caso da estruturas C, sabe-se que:

• parta da estrutura anterior (Exercício 07), definida pós duas superfícies geradas por quatro espirais e por quatro círculos
• desenhe um novo padrão C e aplique-o à geometria

No caso da estruturas D, sabe-se que:

• parta da estrutura anterior (Exercício 07), definida pós duas superfícies geradas por quatro espirais e por quatro círculos
• desenhe um novo padrão D e aplique-o à geometria

No caso do Tentáculo, sabe-se que:

• a circunferência exterior tem um raio de 20 unidades
• a circunferência interior tem um raio de 5 unidade e está à cota cinco
• determine a superfície ferida pelas duas curvas, sabendo que a mesma terá de ser do tipo Normal com uma definição de 10 pontos
• edite a superfície de forma a que esta fique com a configuração uma campânula
• crie uma segunda superfície a partir da primeira e introduza algumas alterações
• desenhe o módulo a partir de um quadrado de 10x10 unidades
• dentro do quadrado e segundo o eixo dos Y's, desenhe 1o linhas do tipo freeform, cujos inicio e fins tenham uma equidistância de 1 unidade
• faça a extrusão dessas linhas segundo Z, com uma altura de 8 unidades
• faça uma segunda extrusão das anteriores superfícies, segundo uma linha auxiliar com 9.15 unidades, ao longo do eixo dos X's

No caso do Tentáculo, sabe-se que:

• a c…