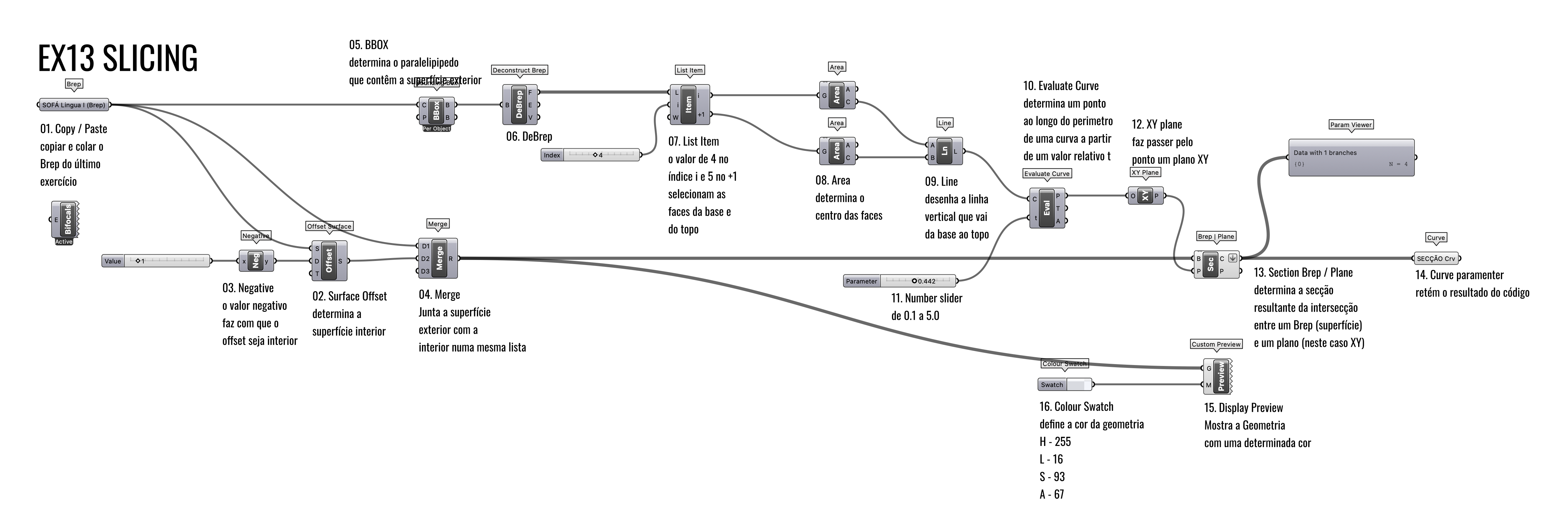
EXERCÍCIO 01
Construção de Superfícies complexas a partir da Morfogénese de Cefalópodes
Tendo em conta que a forma geométrica de cada uma destas conchas é definida por meio de duas diretrizes planas (espirais concêntricas) e por geratrizes definidas por círculos existentes em planos perpendiculares ao plano que contém as directrizes.
EX01.1 Morfogénese: Spirula
EX01.2 Morfogénese: Planorbis
EX01.3 Morfogénese: Nautilus



EX01.1 Morfogénese: Spirula
No caso da Spirula, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior e o ponto A ao seu quadrante direito;
- pelo ponto O, no centro da figura anterior, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a espiral exterior tem centro no ponto O e raio maior no ponto A (15 unidades);
- a espiral interior tem centro também em O e o raio maior é igual a 8 unidades (o seu extremo é o ponto B);
- o número de voltas de ambas as espirais é igual a 2 e ambas se desenvolvem no sentido horário (do centro para o exterior);
- a geratriz é definida por uma circunferência vertical, cujo diâmetro passa pelos pontos A e B.


EX01.2 Morfogénese: Planorbis
No caso do Planorbis, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- para se construir a espiral que irá servir de base à morfogénese da concha é necessário fazer 4 construções auxiliares
- fase I
- desenhar quatro circunferências verticais cujos diâmetros são respectivamente 1, 2, 4 e 8 unidades;
- estes círculos são desenhados, partindo do ponto O até terminar no ponto A e os seus quadrantes são coincidentes entre si;
- estas circunferências fazem parte das geratrizes que definem a forma final;
- fase ii
- desenhar mais três circunferências verticaiscujos diâmetros são respectivamente 1,5 ; 3,0; e 6,0 unidades;
- estes círculos são desenhados, partindo do ponto O para o ponto H e os seus quadrantes também são coincidentes entre si;
- estas circunferências fazem parte das geratrizes que definem a forma final;
- fase III
- defina o pontos B como o quadrante do lado esquerdo do círculo de 6 unidades de diâmetro;
- defina os pontos D, F para os quadrantes que se intersectam na fase II;
- defina os pontos G, E, C para os quadrantes que se intersectam na fase I;
- desenhe vários círculos planos segundo pontos do seu diâmetro (AB, BC, CD, DE, EF, FG e GO);
- fase IV
- desenhe uma linha de H a A
- corte os círculos definidos na fase III pela linha da fase IV, eliminando a parte do quadrante inferior dos círculos AB, CD, EF e GO, e a parte do quadrante superior dos círculos BC, DE e FG.
- os segmentos resultantes dos cortes definidos anteriormente são as directrizes para o planorbis.
EX01.3 Morfogénese: Nautilus
No caso da Nautilus, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a espiral directriz é igual ao do exercício 1.2
- as geratrizes são círculos verticais definidos segundo dois pontos que contêm o respectivo diâmetro
- serão utilizadas 4 geratrizes, que têm em comum o ponto O e cujo diâmetro é respetivamente de 1, 3, 7 e 15 unidades;
- a segunda espiral directriz é definida através dos pontos do quadrante superior das 4 geratrizes e pelo ponto O.

EXERCÍCIO 02
Construção de Superfícies complexas a partir da Morfogénese de Gastrópodes
Tendo em conta que a forma geométrica de cada uma destas conchas é definida por meio de duas diretrizes (uma espiral plana e uma espiral torta assente sobre uma superfície de revolução ou por um eixo vertical) e por geratrizes definidas por círculos existentes em planos perpendiculares ao plano horizontal
EX02.1 Morfogénese: Caracol
EX02.2 Morfogénese: Caramujo
EX02.3 Morfogénese: Búzio



EX02.1 Morfogénese: Caracol
No caso do Caracol, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior e o ponto A ao seu quadrante direito;
- pelo ponto O, no centro da figura anterior, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a geometria desta concha é definida por 4 círculos verticais;
- o maior dos círculos têm um diâmetro de 15 unidades e passa pelo ponto O e A
- o ponto B é definido pelo quadrante superior do circulo OA anterior
- o ponto V, é definido pela lina horizontal perpendicular ao eixo OP que passa pelo ponto B
- as demais geratrizes têm diâmetros, respectivamente, de 1, 3 e 7 unidades e são tangentes ao eixo vertical OP e à linha VB
- a primeira directriz é a gerada por uma espiral plana análoga, mas não igual em dimensão, àquela defenida no exercício 1.3, que é projetada sobre uma superfície de revolução auxiliar;
- a superfície de revolução auxiliar é definida pelo eivo vertical OP e pela geratriz AV;
- a segunda directriz é o segmento vertical definido entre os pontos OV.


EX02.2 Morfogénese: Caramujo
No caso do Caramujo, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 35 unidades, cujo topo é o ponto P;
- uma das geratrizes é um circulo vertical definido pelo seu diâmetro, através dos pontos OA
- as demais geratrizes têm raios iguais a 3,5; 1,5 e 0,5 unidades e são sempre tangentes ao eixo vertical OP e à secção anterior
EX02.3 Morfogénese: Búzio
No caso da Nautilus, sabe-se que:
- a circunferência que envolve toda a geometria tem um raio igual a 15 unidades;
- o ponto O corresponde ao centro da figura anterior, o ponto A ao seu quadrante direito e ponto H ao seu quadrante esquerdo;
- pelo ponto O, passa um eixo vertical com 10 unidades, cujo topo é o ponto P;
- a espiral directriz é igual ao do exercício 1.2
- as geratrizes são definidas por um quadrado de 15 x 15 unidades, o qual se encontra dividido por dois quadrados, respectivamente no canto superior esquerdo e no canto inferior direito
- o quadrado do canto superior esquerdo tem 3 x3 unidades e contem um quarto de circulo cujo centro é o canto inferior direito
- o quadrado do canto inferior direito tem 12 x 12 unidades e contei um quarto de circulo cujo centro é o seu canto superior esquerdo
- no canto superior direito existe um rectângulo de 12 x 3 unidades, o qual contem um arco de clips, com centro no sei canto inferior esquerdo e raios iguais aos lados
- ao prolongar-se o lado esquerdo do quadrado de 15 x 15 unidades, este vai ser tangente a um circulo de raio igual a 15 unidades , o qual também é tangente ao arco existente no quadrado de 12 x 12 unidades
- as geometrias existentes no quadrado de 3 x 3 e no rectângulo de 12 x 3 devem ser unidas, correspondendo o lado esquerdo ao ponto O e o lado direito ao ponto A
- as geometria resultantes do prolongamento do lado esquerdo do quadrado de 15 x 15, do circulo de r= 15 e do quadrado de 12 x 12 devem ser unidas numa única curva, sendo o seu extremo inferior esquerdo o ponto P e o seu extremo direito o ponto A
- estas duas últimas figuras geométricas devem se rodadas 90 segundo a charneira definida pelos pontos OA
- a superfície de revolução auxiliar é um arco de elipse (1/4) vertical com centro no ponto O, semi-eixo horizontal em A e semi-eixo vertical com 5 unidades.

EXERCÍCIO 03
Construção de Superfícies complexas a partir da Morfogénese de Bivalves
Tendo em conta que a forma geométrica de cada uma destes bivalves é definida por meio de duas diretrizes (uma semicircunferência vertical e uma curva cónica) e por geratrizes definidas no plano horizontal
EX03.1 Morfogénese: Mexilhão
EX03.2 Morfogénese: Vieira
EX03.3 Morfogénese: Ostra


EX03.1 Morfogénese: Mexilhão
No caso do Mexilhão, sabe-se que:
- o rectângulo que contêm a forma em planta tem 8 x 20 unidades
- dentro desse rectângulo existem mais 4 sub-rectângulos localizados nos extremos
- o sub-rectângulo do canto inferior esquerdo é um quadrado com 3x3 unidades
- o sub-rectângulo do canto inferior direito é um quadrado com 5x5 unidades
- o sub-rectângulo do canto superior esquerdo tem 3 x 17 unidaes
- o sub-rectângulo do canto superior direito tem 5 x 15 unidades
- nas figuras que são quadrados gere um arco de circunferência
- nas figuras que são rectângulos, gere elipse
- por fim una os quatro segmentos numa única curva


EX03.2 Morfogénese: Vieira
No caso do Vieira (nervuras), sabe-se que:
- em planta a vieira é definida por um rectângulo de 10 x 9 unidades
- o rectângulo anterior é subdividido em 4 rectângulos mais pequenos, localizados em cada um dos extremos
- nos extremos inferiores os sub-rectângulos são quadrados de 5 x 5 unidades
- nos extremos superiores os sub-rectângulos têm 4 x 5 unidades
- existe ainda um quinto sub-rectângulo de 4 x 2 unidades em que o centro coincide com o ponto médio do segmento superior do rectângulo envolvente
- nos sub-rectângulos são quadrados de 5 x 5 unidades gere dois arcos de circunferência
- nos sub-rectângulos têm 4 x 5 unidades gere dois arcos de elipse
- uma a quinta sub-rectângulo às elipses
- uma as dois arcos de circunferência por forma a gerar um semicirculo
- subdivida-o em 25 partes e faça passar por cada dois pontos um circulo
- corte os últimos círculos segundo o semicírculo anterior
- junte todas as semicircunferências com as elipses
EX03.3 Morfogénese: Ostra
No caso da Ostra, sabe-se que:
- o rectângulo que contem forma em planta tem 20 unidades (em X) por 9 unidades (em Y)
- subdivida o rectângulo anterior em 6 subrectângulos
- gere um rectângulo de 5 x 10 unidades por forma a coincidir com os cantos inferiores esquerdo e direito;
- em cada um destes dois rectângulos gere um arco e elipse
- a parte superior é definida por 4 rectângulos, todos com 4 x 5 unidades
- nos rectângulos dos extremos superiores gere arcos de elipse
- e nos rectângulos centrais dos segmentos de recta, coincidentes com a parte superior desses mesmo retângulos
- uma os dois segmentos de elipse existentes no lado esquerdo e repita o processo para o lado direito
- faça passar pós cada uma das anteriores curvas unidas uma espiral segundo uma curva, definindo que o raio inicial (no ponto médio inferior) tem um raio de 1 unidade e que no outro extremo um raio com 0 unidades

EXERCÍCIO 04
EX04 Morfogénese: Corais
No caso da estrutura A, sabe-se que:
- Desenhe duas circunferências com o mesmo centro, em que uma das circunferências tem 2 unidades de raio e a outra 4 unidades
- copie as duas circunferências 12 unidades para o lado direito
- em cada um dos dois conjuntos de círculos desenhe uma linha vertical ao plano de trabalho com 6 unidades
- desenhe um arco de circunferência por forma a unir os extremos superiores das linhas verticais
- una os dois segmentos verticais ao arco de circunferência anterior
- desenhe quatro espirais à volta do eixo (figura anterior) partindo dos quadrantes esquerdo e direito de cada circulo, perfazendo uma volta
- gere duas superfícies, uma interior e outra exterior, com base nas directrizes definidas pelas espirais e pelas geratrizes definidas pelos círculos
- desenhe um padrão A, B e C e aplique-os à geometria
Construção de Superfícies complexas a partir da Morfogénese de estruturas de Corais

EXERCÍCIO 05
EX05 Morfogénese: ANÉMONAS
No caso da estruturas A, sabe-se que:
- Desenhe um rectângulo com 30 por 30 unidades
- Transforme esse rectângulo num plano
- Redifina a densidade dos pontos u,v em 5 por 5 através do Revuild
- Manualmente altere os pontos de control da superfície de modo a deformá-la.
- copie a superfície anterior em Z 5 unidades e deforme a nova superfície

EXERCÍCIO 08
EX08 Morfogénese: Fotografia Paramétrica




EXERCÍCIO 10
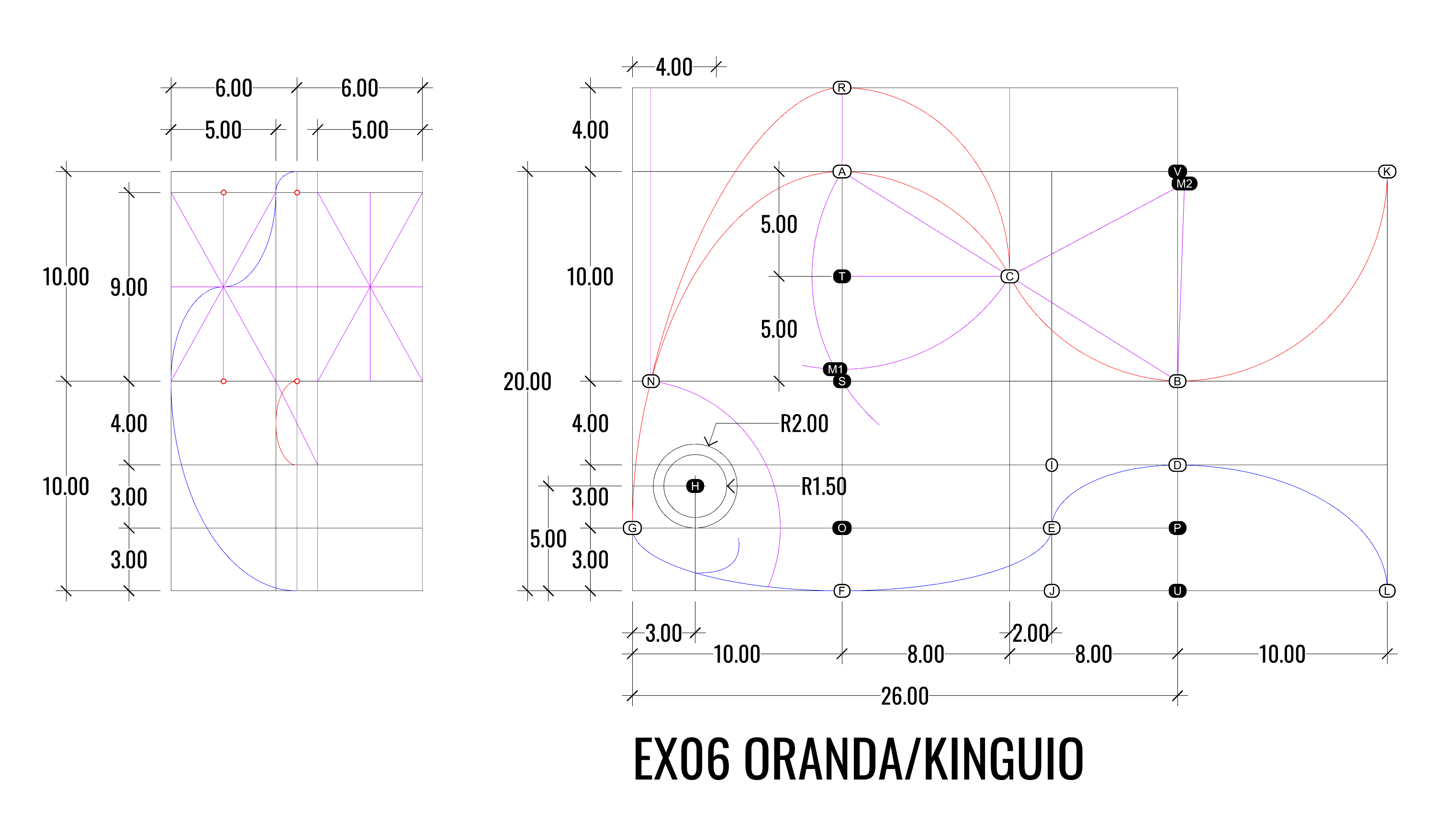
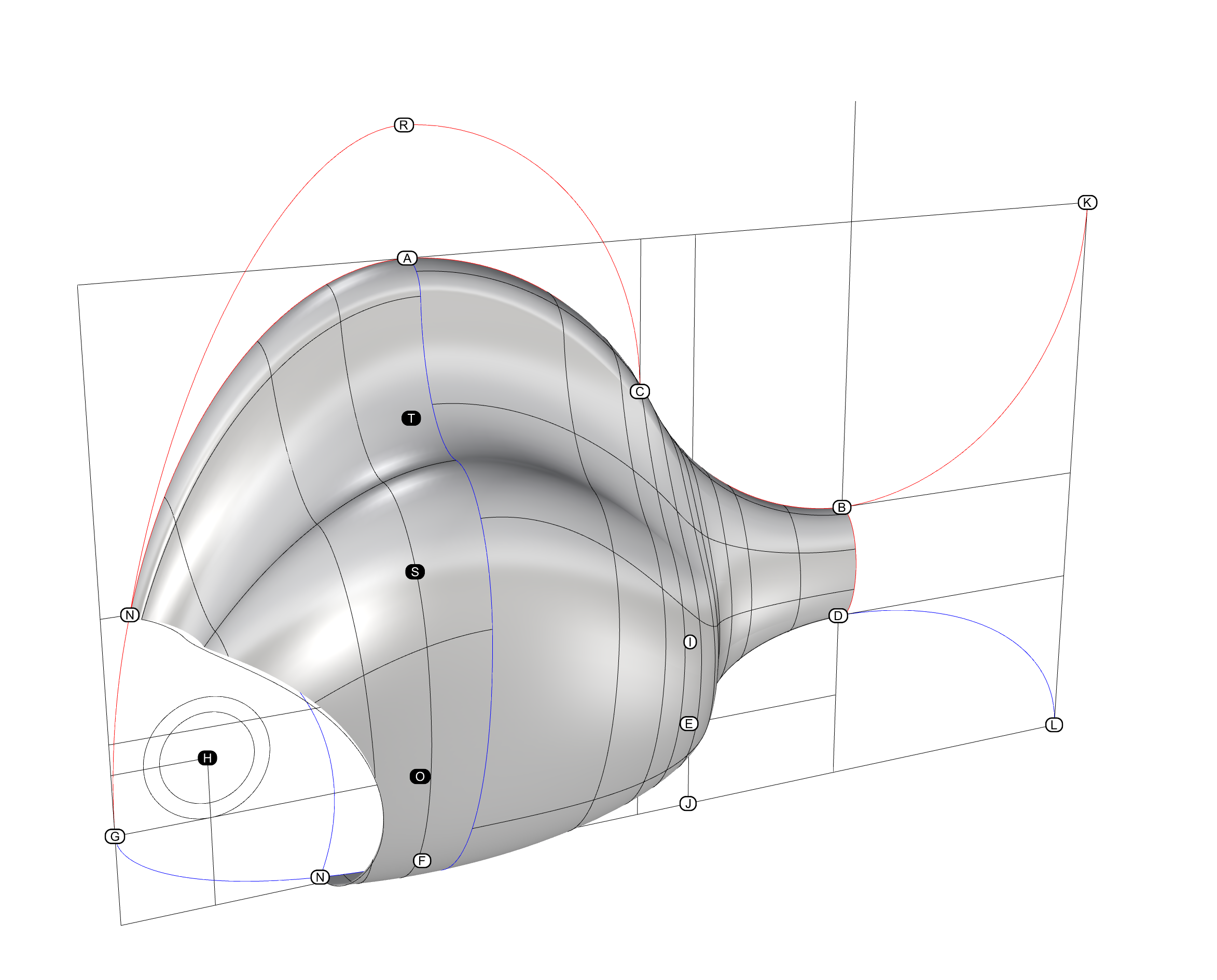
EX10 Morfogénese: Banco Paramétrico II
Considera as seguintes variáveis e intervalos de valor:
- O perfil lateral do banco está inscrito num quadrilátero em que o canto inferior esquerdo é o ponto de coordenadas 0,0,0
- Considera que o perfil lateral tem uma forma de L invertido, sendo o ponto inferior direito dessa figura o ponto A
- O perfil do banco é constituído pelos pontos A a F, definidos no sentido contrário aos ponteiros do relógio
- Os ponto G e H, correspondem \à posição relativa da secção circular que inclui as costas
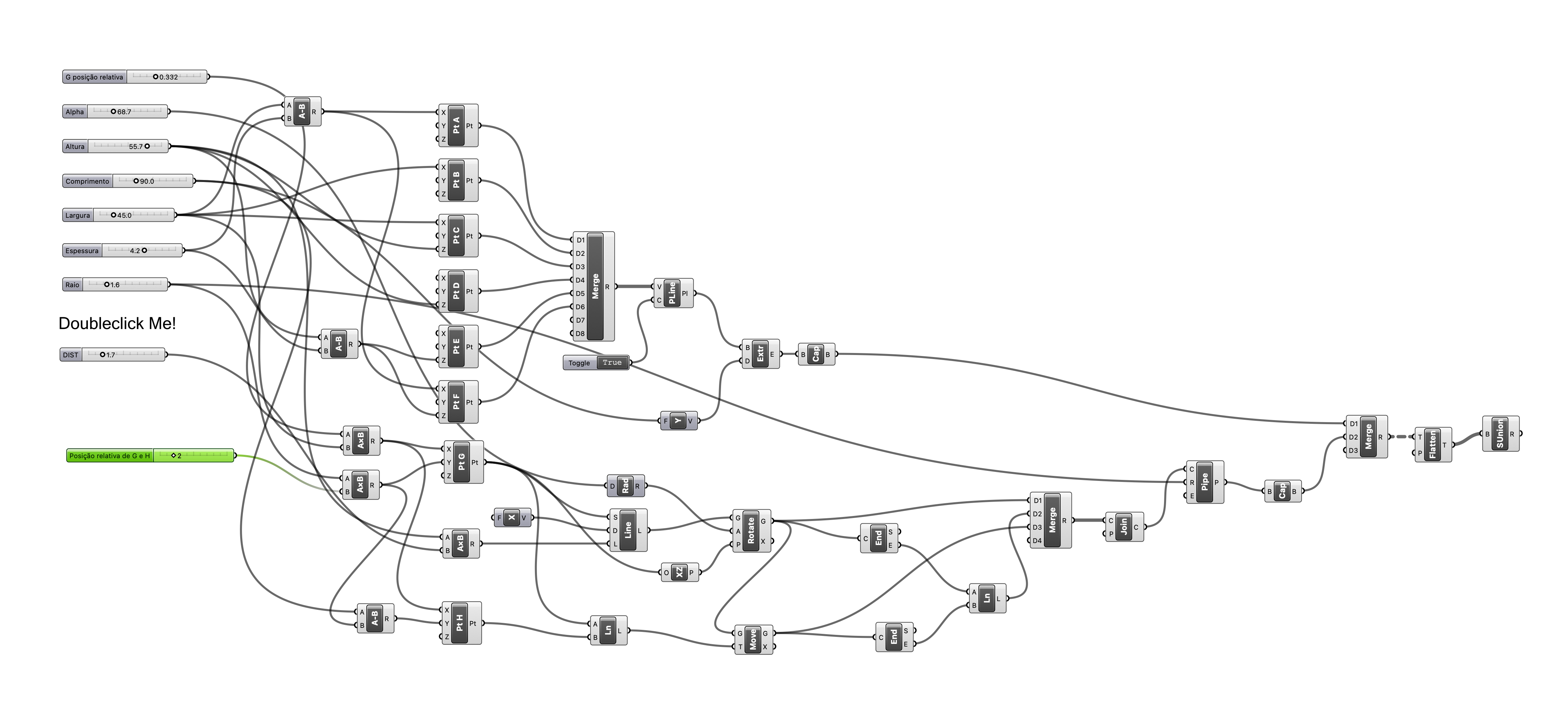
- Altura - altura do banco [40<60.0]
- Largura. - largura do banco [40<65.0]
- Comprimento - comprimento do banco [60<180.0]
- Espessura - espessura do assento [1<7.0]
- Raio - raio do perfil circular [0.5<5]
- Posição G - posição relativa do ponto G e H, relativamente à largura total [0<1.000]
- Alpha - ângulo definido pelas pernas com o plano horizontal [60<90.0]
- DIST - dimensão das pernas, é um factor de multiplicação em relação à altura do banco [1.5<2.5]
- O afastamento do ponto G e H, segundo o eixo dos Y, relativamente à implantação do banco é igual a das vezes o Raio


EXERCÍCIO 11
EX11 Morfogénese: Sofá I
Modele em Rhino uma forma geométrica que apresente as mesmas características tipológicas que a figura abaixo


EXERCÍCIO 15
EX15 Objeto gerado através de MDF KERFING
Construa um modelo (de um Relógio, Pulseira, Colar ou Abajur) em Rhino de modo a empregar uma ou mais abordagens através de MDF Kerfing
EX15.1 Conceito
Defina:
- qual o objeto a prototipar (Relógio; Pulseira; Colar; Abajur/Candeeiro)
- Defina o Conceito e Princípio da "mola a utilizar, por forma a tornar a placa de MDF 3mm flexivel;
- Insira imagens ou padrões em que se inspirou;
- Desenhe à mão levantada a estrutura de "molas" a utilizar, dando uma visão do objeto planificado e em uso
EX15.2 Desenho técnico 2D
Gere:
- O módulo de mola de que vai utilizar;
- Represente o desenho a "D da planificação do objeto à escala real, com o fecho utilizado;
EX15.3 Protótipos preliminares
Fabrique:
- um ou mais protótipos preliminares, por forma a identificar as fraquezas e os pontos fortes;
- Insira fotos dos mesmos planificados e em uso;
- insira esquemas de avaliação do modelo produzido;
EX15.4 Protótipos Final
Fabrique o protótipo final:
- inclua 4 fotos do mesmo, sendo uma foto do modelo planificado; 2 fotos em uso; 1 foto do fecho na posição de uso
- inclua o desenho técnico 2D a p&b
- inclua representação tridimensional em Rhino do modelo em uso (lembre-se do comando FLOW) em 4 perspectivas diferentes
- inclua o desenho a prototipar, com as respectivas cores
- pequena "brochura" final da sua proposta